Les Types D'action En Régulation

La régulation est essentielle pour les circuits frigorifiques et permet de nombreuses actions nécessaires au fonctionnement du système. La régulation peut également compenser un certain nombre de mauvais fonctionnements liés à la conception ou à la mise en oeuvre de ces circuits. Toutefois l'objectif principal est d'adapter au plus proche la production aux besoins.

Le système mis en oeuvre pour la régulation est constitué principalement :

- d'un capteur (température, pression, etc.),

- d'un régulateur,

- d'un organe de réglage.

Le capteur va mesurer la grandeur à contrôler et envoyer l'information au régulateur. Le régulateur compare l'information avec le point de consigne (grandeur souhaitée). Le résultat de cette comparaison est appelé écart ou encore erreur. Le régulateur va appliquer un algorithme de régulation à l'erreur afin de pouvoir transmettre un signal à l'organe de réglage dont la fonction est d'agir sur une capacité dans le but in fine de corriger l'erreur.

L'organe de réglage peut être une vanne de réglage, un compresseur etc. La manière dont la grandeur mesurée est influencée par l'organe de réglage détermine le type de boucle de régulation. On distingue :

-La boucle ouverte : le capteur ne mesure pas la grandeur dans l'endroit où l'organe de grandeur agit. L'utilisation d'une boucle ouverte peut être due à la difficulté de mesurer la grandeur régulée (chauffage central d'un immeuble avec sonde extérieure par exemple) ou à la connaissance du système régulé.

- La boucle fermée : le capteur mesure la grandeur dans l'endroit où l'organe de grandeur agit. Dans ce cas, on contrôle la grandeur souhaitée via l'erreur et on effectue les corrections nécessaires au fil du temps (climatisation d'une pièce avec une sonde d'ambiance par exemple).

Les régulateurs ont fortement évolué ces dernières années. Ces évolutions se sont traduites par des appareils moins chers, plus fiables et performants. Par ailleurs, des fonctions supplémentaires qui relevaient de fonctionnalités avancées sont devenues communément natives (port de communication avec les régulateurs électroniques par exemple). De même, les fournisseurs proposent une large gamme dans laquelle la quasi-globalité des algorithmes est abordée.

La figure 1.1 schématise un régulateur électronique avec une entrée et une sortie. Le régulateur peut comporter un grand nombre d'entrées et de sorties avec plusieurs algorithmes permet- tant ainsi des fonctions diverses telles que la régulation de la température d'une chambre froide, la gestion des dégivrages, les alarmes sur détection de seuil... Le régulateur peut disposer de sorties supplémentaires (autres que pour l'organe de réglage) pour des fonctions telles que la recopie de lecture, l'alarme, la communication...

schéma d'un régulateur à une entrée et à une sortie

Dans la majorité des cas, l'algorithme utilisé est classiquement du Tout Ou Rien (TOR). L'utilisation du TOR reste simple et l'arrêt).Les régulateurs TOR sont généralement du type mécanique mais pas seulement, et cette régulation apporte dans la large majorité des cas la satisfaction désirée. Cependant, on peut être amené en fonction de l'application à utiliser d'autres lois afin de minimiser l'erreur.

On fait alors fréquemment appel à la régulation proportionnelle (P) qui commande un organe proportionnel (vanne deux voies ou trois voies par exemple).

L'avènement et la généralisation de l'électronique ont permis d'ajouter des correcteurs à la régulation proportionnelle, en la Dans certains cas (zone à risque d'explosion par exemple), on supprime les sources d'ignition.

1.1 Régulation Tout Ou Rien

La régulation Tout Ou Rien enclenche (Tout) ou arrête (Rien) l'organe de réglage. Par conséquent, on cherche à atteindre la grandeur souhaitée en utilisant l'organe de réglage entre sa capacité maximale et minimale.

Il en résulte un encadrement qui sera d'autant plus conséquent entendu qu'un réglage d'encadrement faible générera, entre autres, des courts cycles sur l'organe de réglage. Cet encadrement est appelé différentiel. Le régulateur se paramètre en fixant un point de consigne et un différentiel.

Le point de consigne correspond à la grandeur souhaitée (basse ou haute selon le régulateur). La figure 1.2 montre l'évolution sinusoidal de la grandeur en fonction du temps pour une régulation avec des caractéristiques de refroidissement.

La courbe représentant l'évolution de la grandeur dans le dépasse l'encadrement schématisé par les droites perpendiculaires à l'axe des abscisses.

Ce phénomène est dû aux différentes inerties du système engendrées notamment par:
- le temps de réaction du régulateur,
- le temps de réaction de l'organe de réglage et sa mise en température (à l'arrêt comme à l'enclenchement).

Par conséquent, le résultat obtenue n'est pas réellement celui souhaité.
On pourrait objecter qu'une des solutions consiste à diminuer la valeur du différentiel; cependant, cette correction n'est valable que dans la limite du pompage du système, le pompage du système générant de toute manière une oscillation de la grandeur en « stressant » l'organe réglage. Le différentiel est donc un compromis entre l'absence de pompage et l'encadrement le plus faible de la grandeur désirée.

Il y a lieu de noter que certaines applications peuvent utiliser un différentiel conséquent intrinsèquement à leur fonctionnalité. A ce titre, on peut citer des applications avec le thermostat de fin de dégivrage (chapitre 9, Dégivrage ») ou encore le réfrigérateur électroménager classique à deux compartiments sur un seul circuit frigorifique.

1.2 Action proportionnelle (P)

La regulation proportionnelle agit sur un organe qui accepte se s'adapter proportionnellement, un variateur de vitesse par exemple. On peut donc faire appel à cette régulation en fonction de l'organe à commander ou parce qu'une autre régulation (TOR par exemple) ne donne pas la satisfaction souhaitée. L’Algorithme proportionnel consiste à délivrer un signal proportionnel à l’organe de réglage en fonction de l’erreur (entre la consigne et la mesure).

L'action proportionnelle est déterminée par la bande proportionnelle fixant la valeur de l'erreur pour laquelle le signal de sortie est de 100 %. Le réglage d'un régulateur proportionnel s'effectue en paramétrant le point de consigne et la bande proportionnelle (ou le gain selon le régulateur). A l'instar du différentiel de la régulation TOR, la valeur de la bande proportionnelle doit être fixée à la valeur la plus faible obtenue sans phénomène de pompage.

Majoritairement, le point de consigne est donné au signal à 0 % ; toutefois, certains fabricants considèrent que le point de consigné est à 50 % du signal. On voit toute l'importance de se référer à la documentation du fabricant pour connaître les points de réglage. Le signal à 0 % est obtenu avec une erreur de 0. Toutefois, la valeur de 0 % est relative et ne correspond pas forcément à un signal à 0 % (le signal 4-20 mA donne 4 mA à 0 % par exemple).

La figure 1.3 indique un signal proportionnel destiné à commander une vanne trois voies sur une batterie alimentée en frigo- porteur négatif. Il y a lieu de noter que le signal croît avec l'augmentation de la grandeur mesurée : l'évolution est dite « directe » (refroidissement). Lorsque le signal décroît avec l'augmentation de la grandeur mesurée, l'évolution est dite « inverse » (chauffage).
Certains régulateurs permettent d'effectuer des évolutions directes et inverses; d'autres ont un fonctionnement figé selon l'une ou l'autre de ces évolutions.

Erreur rémanente (ou statique)
La régulation proportionnelle agit en permanence proportionnellement à la valeur de l'erreur (soit en décalage). Par ailleurs, les besoins trouvent une compensation via la capacité de l'organe de réglage. Par conséquent, les besoins vont rentrer au fil du temps en adéquation avec la capacité de l'organe de réglage et donc figer dans le temps la valeur de l'écart.

À titre d'exemple, si on considère dans le schéma précédent que la vanne est ouverte à 50 % et qu'elle délivre exactement de quoi compenser les déperditions nécessaires, la grandeur mesurée sera figée à-7,5 °C.
Cette erreur est appelée erreur rémanente ou erreur statique et sera présente dès que les besoins seront supérieurs à 0 %. L'erreur rémanente est préjudiciable dans le cas où l'on souhaite s'approcher le plus près possible de la grandeur au signal à 0 %. Il sera donc nécessaire d'utiliser des fonctions supplémentaires pour limiter voire annihiler cette erreur.

1.3 Action intégrale (I)

La fonction intégrale est focalisée sur le traitement de l'erreur rémanente. Cette fonction mathématique bien connue est rendue possible grâce à l'électronique des régulateurs. L'erreur rémanente va être moyennée suivant un temps donné et un signal correctif va s'ajouter au signal proportionnel.
On cherche donc à « déstabiliser » de réglage augmente alors sa capacité pour que l'erreur se réduise puis s'annule. Toutefois, cette action est lente et ne s'effectue qu'au fil du temps. signal par un ajout : l'organe Le réglage de la fonction intégrale porte sur le temps d'intégration. Une valeur trop faible engendrera des instabilités du système alors qu'une valeur trop élevée annulera l'action de l'intégrale.
À noter Il est à signaler qu'à la mise en service d'une installation, l'erreur est très élevée et risque de générer une action intégrale disproportionnée. Cette action peut se solder par un dépassement de consigne. Aussi afin d'éviter æ type de phénomène, les régulateurs suppriment généralement l'action de l'intégrale lorsque l'erreur est supérieure à la bande proportionnelle.

1.4 Action dérivée (D)

Si l'action de l'intégrale résout dans le temps les erreurs rémanentes liées à la régulation proportionnelle, il n'en reste pas moins qu'il s'agit toujours d'une action de correction a posteriori. De même, nous avons vu précédemment que l'action proportionnelle réagir à une erreur, Il n'y a donc aucune anticipation dans le cas d'une boucle fermée et on ne réagit que face à un constat d'erreur.

La fonction dérivée a pour objet de traiter ce point en calculant, via le régulateur électronique, la variation dans le temps de l'erreur (fonction mathématique dérivée). Le résultat de ce calcul donne une correction au régulateur afin que l'organe de réglage fournisse plus de capacité. L'action dérivée deviant nulle lorsque l'erreur devient constante.

Le réglage de la fonction porte sur le temps de dérivée. Un temps égal à 0 donnera une action nulle et un temps élevé générer a une action conséquente. Compte tenu que la fonction dérivée est une action rapide due à la variation de l'erreur dans le temps, on conçoit que la représentativité de la grandeur mesurée est fondamentale.

Aussi, la mesure devra être absente de bruits parasites qui pourraient être la source d'instabilités de fonctionnement. De même, un mauvais filtrage de la grandeur mesurée rendra caduque la fonction. A l'opposé de la fonction intégrale, la fonction dérivée peut être active hors bande proportionnelle.

1.5 Action proportionnelle, intégrale et dérivée (PID)

Un régulateur PID a pour fonction les trois actions suivantes:

• --Proportionnelle,
• --Intégrale,
• --Dérivée.

Pour un régulateur PID, il existe plusieurs possibilités d'associer les actions intégrales er dérivées à la régulation proportionnelle.
On note:

1. - PID série,
2. - PID parallèle,
3. - PID mixte.

Les figures ci-après représentent ces différentes architectures.

1.6 Expression mathématique d'un PID mixte

1.6.1 Action proportionnelle

avec :
Y = signal de sortie
C = signal de sortie pour un écart égal à 0
Kp = constante de proportionnalité
φ = écart entre le point de consigne et la grandeur mesurée

1.6.2 Action proportionnelle et intégrale

avec :
Y = signal de sortie
C = signal de sortie pour un écart égal à 0
Kp = constante de proportionnalité
φ = écart entre le point de consigne et la grandeur mesurée
ti = temps d'intégration

1.6.3 Action proportionnelle, intégrale et dérivée

avec
Y = signal de sortie
C = signal de sortie pour un écart égal à 0
Kp = constante de proportionnalité
φ    = écart entre le point de consigne et la grandeur mesurée
ti = temps d'intégration
td = temps dérivé

1.7 Méthode Ziegler Nichols (boucle fermée)

La modélisation de système débouchant sur les réglages d'un PID est fastidieuse et nécessite des connaissances étendues. En pratique, les PID font souvent l'objet de réglages empiriques ou appellent à des méthodes de réglage expérimentales in situ.

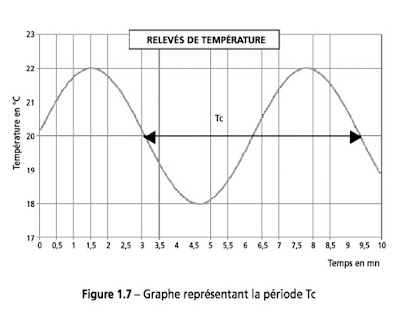
Une de ces méthodes est celle de Ziegler Nichols, qui se bate sur la limite de pompage du régulateur. Elle consiste à régler Kc(obtenue en limite de pompage) avec Ti: +∞ et Td: 0. On mesure alors la période Tc correspondante aux cycles de pompage obtenu.

A l'aide du Kc et Tc, on applique les coefficients suivants en fonction du régulateur qui s’applique au PID mixte à paramétrer.